Rectilinear Crossing Number
Tím BOINC.SK

Rectilinear Crossing Number je matematický projekt, ktorý sa snaží vyriešiť rôzne výpočtové a kombinačné problémy vychádzajúce z konečného počtu bodov v Euklidovej rovine.
Sem patrí niekoľko problémov z teórie grafov, v ktorých spojnice medzi akýmikoľvek dvoma bodmi sú priame (pod pojmom graf v tomto prípade rozumieme abstraktné znázornenie skupiny objektov, kde niektoré z nich sú navzájom spojené).
Základná otázka znie: aký je najmenší počet priesečníkov v grafe, ktorý vznikol vzájomným prepojením všetkých n bodov v rovine priamymi spojnicami? Uvažujeme všeobecné rozloženie bodov v rovine, kde tri rôzne body neležia na jednej priamke.
Je jednoduché umiestiť 4 body tak, aby sa ich spojnice nepretínali. Obrazec s piatimi bodmi ukazuje rôzne spôsoby ich zoskupenia. Ak usporiadame 5 bodov do konvexných pozícií, dostaneme 5 priesečníkov. V ideálnom usporiadaní piatich bodov dosiahneme iba jeden priesečník (v pät bodovom grafe nie je možné dosiahnuť 0 priesečníkov, ani keby sme priame spojnice nahradili krivkami). V princípe je jednoduché pre akúkoľvek množinu n-bodov dosiahnuť maximálny možný počet priesečníkov - stačí všetky body umiestniť na kružnicu.
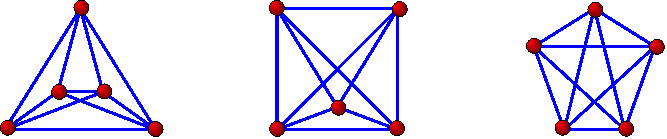
Obr.: Príklady 5 bodových grafov

Pri usporiadaní väčšieho počtu bodov je oveľa náročnejšie nájsť ideálnu konfiguráciu, počet možných usporiadaní rastie exponenciálne s počtom bodov. Napríklad pre n=11 existuje 2,334,512,907 rôznych konfigurácií.
Cieľom projektu Rectilinear Crossing Numbers je nájsť ideáalne usporiadania pre male čísla n, v súčasnosti sa skúma n=18. Priebežné vysledky nájdete na projektovej stránke.
- Ak chcete pridať komentáre, tak sa musíte prihlásiť
- prečítané 19355x


